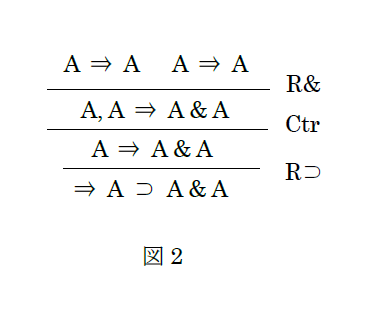前回の日記では、次の回は Curry's Paradox のやや formal な説明を行ないますと述べましたが、その説明の前に、関連しますが別の話題を今日は記します。予定変更ですみません。
先日、次の論文を一通り読み終えたのですが、
- Jc Beall and Julien Murzi ''Two Flavors of Curry's Paradox,'' in: The Journal of Philosophy, vol. 110, no. 3, 2013
これを読んでいて、個人的に意外というか、「あ、そうなんだ。それは知らなかったな。興味深いな。そうなんですね」と感じたことがありましたので、そのことを以下で記してみます。小さなことなのですが、structural rule の Contraction にご興味を持っておられる方は、頭の片隅にでもとどめておいた方がよさそうなことです。その筋の専門家の方はみなさん既にご存じなのかもしれませんが、私は先日初めて教えられました。
さて、上記の論文の p. 146, footnote 10 を見ると、次のように書かれていました。読んでみて軽く驚きました。
Multiple discharge of assumptions in a natural deduction framework is in effect equivalent to Structural Contraction. See Sara Negri and Jan von Plato, Structural Proof Theory (New York: Cambridge, 2001), chapter 8.
「えっ!? 自然演繹の証明で同じ仮定を同時に複数落とすことは、Sequent Calculus で言えば structural rule としての Contraction を使っているに等しい!? ほんとですか!? それは知らなかったな」と、若干意外の念に打たれました。そこでさっそく自室にある Structural Proof Theory の Chapter 8 を開いてみました。この本は購入しておきながら、積読になっておりました。開いてみると8章の冒頭の page に次のようにありました。Gothic は原文にある通りです。
We shall show in detail that […] contraction is the same as multiple discharge [of assumptions].*1
そして、さらに page を繰ると、自然演繹の multiple discharge が Sequent Calculus の Contraction の適用であることがわかる証明図が出ていましたので (p. 178.)、それを以下に掲示してみます。
まず、自然演繹で同じ複数の仮定を同時に落とす簡単な証明の例です*2。「図1」というのは引用者によるものです。原文には証明図に名前が付いていません。
最終行を導く際に、図の頭にある 1. という名の二つの A が同時に落とされています。次はこの証明図に対応する Sequent Calculus の証明図です。
おおっ! 出てきました。上から3行目の式を導く際に Contraction (Ctr) が使われているのがわかります。本当に使われていますね。
そこで、これらの図を受けて、私の方で自然演繹の証明図に、無理矢理 Contraction の規則を適用していることを明示する行を入れてみました。次がそれです。これは Structural Proof Theory には出ていない図です。
二つの同じ A に別々の名前 1., 2. を付け、それらをそれぞれ順番に落とし、最終行を導く際に Contraction を使用して、上記、図1 の最終行と同じ式を引き出しています。なるほど、こんなふうになっていたんだ。知らなかったな。
かつて、自然演繹で証明を書き下す際に、同じ仮定を同時に複数落とすとき、「どうして同時に複数落としていいのだろう?」と疑問に思ったことがありました。でも「そういうものなのだろう」と感じただけで、深く考えたこともなかったのですが、どうやら structural rule としての Contraction がその根拠にあるということみたいですね。「Contraction よ。お前はそこにもいたのか!」という感じです。この rule は知らぬ間にあちこちに遍在しているようですね。
以上です。間違ったことを書いておりましたらすみません。私は論理学が苦手ですので、ひどい誤解や勘違いをしている可能性がございます。正確には上記の Structural Proof Theory に当たってみてください。誤字、脱字等にもお詫び申し上げます。
次回はたぶん Curry's Paradox の若干 formal な説明を行ないたいと思います。たぶんですが…。
*1:Sara Negri and Jan von Plato, Structural Proof Theory, with an Appendix by Aarne Ranta, Cambridge University Press, 2001, p. 165.
*2:以下の証明図において、& と ⊃ では & の方が結合力が強いです。