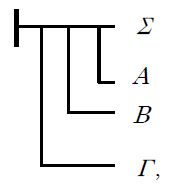目次
- 1. 推論規則 Modus Ponens
- 2. 推論規則 Ex Falso Quodlibet/Ex Contradictione Quodlibet (EFQ/ECQ)
- 3. EFQ/ECQ の形式的証明
- 4. 問題: Frege は EFQ/ECQ を認めたか?
- 5. Frege の証言
- 6. Frege は EFQ/ECQ を認めなかったであろう。
- 7. まとめ
ささいなことながら、個人的に意外に思ったことを一つ、記してみたいと思います *1 。昔の論理学者が、ある推論規則を支持したか否か、ということについて書いてみます。間違ったことを書いていましたら、すみません。(読み始める前に、全体の概要を知りたいというかたは、本文終りにある「7. まとめ」の節をご覧ください。)
1. 推論規則 Modus Ponens
先日、次の文献を読んでいて、気付かされました。
・ Curtis Franks ''The Context of Inference,'' in: History and Philosophy of Logic, vol. 39, no. 4, 2018.
Modus Ponens (MP) という推論規則があります。
任意の平叙文 p, q について、「p ならば q」と p という二つの前提があれば *2 、q という結論を引き出してよい、とする規則です *3 。
たとえばそれは、「明日雨ならば試合は中止である」と「明日は雨である」という二つの前提があれば、「試合は中止である」という結論を引き出してよい、とする規則です。
ここで問題です。昔、ドイツに Gottlob Frege (1848-1925) という論理学者がいましたが、彼はこの MP を推論規則として認めたでしょうか?
Frege について何も知らなくても心配はいりません *4 。これをお読みのかたは「この Modus Ponens という規則は、ごく当たり前に成り立つものだろうから、Frege という人も、成り立つとして認めたのではなかろうか」とお感じだと思います。そう、正解です。彼はこの規則を正しいものとして認めています *5 。
2. 推論規則 Ex Falso Quodlibet/Ex Contradictione Quodlibet (EFQ/ECQ)
ところで、現在、一般に認められている推論規則のうちには、Ex Falso Quodlibet/Ex Contradictione Quodlibet (EFQ/ECQ) と呼ばれるものがあります *6 。
この規則は、間違ったこと/偽であること、あるいは矛盾を前提にすれば、任意のことを結論として引き出してよい、とする規則です *7 。
たとえば「2+2 = 4」かつ「2+2 ≠ 4」という矛盾を前提に取れば、ここから、地球は真っ平らである、という結論を引き出してもよい、ということです。
この規則は、矛盾があればそこから任意のことを引き出してよく、引き出された結論は正しい、とするものですが、これは MP に比べて、ちょっと納得しにくいところがあるかもしれません。
そこで、EFQ/ECQ を正しい規則であるとする、informal で直観的な説明を与えてみましょう。
さて、起り得べからざることには、どんなことがあるでしょうか? 突然巨大な地震が襲うとか、魚が空から降ってくるとか、そのようなことが起り得べからざることとして考えられますが、最も起り得べからざることとは何でしょうか? そうですね、矛盾です。「2+2 = 4 かつ 2+2 ≠ 4」とか「富士山は日本一高い山であり、かつそうではない」というような矛盾です。矛盾こそが最も、最高度に、起り得べからざることです。そこで、そうだとするならば、矛盾が起ったと認めて前提にすれば、あとはどんなことが起っても不思議ではないでしょう。最も起り得べからざることが起ったのだから、あとは何だってありです。何が起ってもおかしくはない。よって、矛盾を前提にすれば、任意のことを結論として引き出してよい、ということになります *8 。
以上の informal で直観的な説明は、雰囲気からすれば飲み込みやすいですが、EFQ/ECQ を正しいとする、雰囲気に流されることのない、formal で厳密な証明があったほうが望ましいことです。
ではその、formal で厳密な証明も与えてみましょう *9 。
3. EFQ/ECQ の形式的証明
矛盾があるならば、任意の文が成り立つことの証明
EFQ/ECQ は、矛盾があれば結論として任意の文を引き出してよい、とする推論規則です。
以下の証明では、最初に矛盾 p ∧ ¬p を仮定し、そこから任意の文 q を引き出します。そうして「矛盾があるならば、任意の文が成り立つ (p ∧ ¬p) → q *10 」を証明します。
ここで、証明に出てくる記号を簡単に説明しておきます。
p, q を任意の平叙文とします。否定を表す記号を ¬ とし、連言「かつ」を ∧, 選言「または」を ∨, 条件法「ならば」を → とします。
それでは証明に入ります *11 。
証明
1. p ∧ ¬p (仮定)
2. p (1. より、連言除去)
3. p ∨ q (2. より、選言導入)
4. ¬p (1. より、連言除去)
5. q (3. と 4. より、選言三段論法 *12 )
6. (p ∧ ¬p) → q (1. の仮定を落とし、5. で条件法導入)
こうして明確に「矛盾があるならば、任意の文が成り立つ」ということ、すなわち EFQ/ECQ (の式の形をした version) が証明できました。EFQ/ECQ は informal な点からも formal な点からも正しいと考えられます *13 *14 。
4. 問題: Frege は EFQ/ECQ を認めたか?
さて、ここで再び問題です。思い出していただきたいのですが、Frege は Modus Ponens (MP) を推論規則として認めていました。それでは彼は EFQ/ECQ を推論規則として認めたでしょうか?
ここから先の話は Frege についての知識が若干必要なのですが、彼は高階の古典論理を認めていたと考えられます *15 。そうしますと、彼は (trivial に) 古典論理を認めていた、ということになります。としますと、古典論理には EFQ/ECQ が含まれますから *16 、彼は EFQ/ECQ を認めていただろうと推測できます。
しかし、ちょっと意外なことに、Frege が EFQ/ECQ を推論規則として認めることは、まずあり得なかったであろう、と考えられるのです。そのことは、彼の遺した文献を証拠として言えるのです。これは、少なくとも私には何だか意外なことでした。「えっ、そうなんだ」という軽い驚きがありました。その証拠を以下に記してみましょう。
Frege が EFQ/ECQ を推論規則として認めるはずがないことがわかる、彼の発言はいくつか残されているのですが、比較的詳しくて明瞭な証言を一つ、彼の著述から引用してみましょう *17 。
その前に、その引用文の内容について、前もって少しお知らせしておきます。
以下の引用文で Frege が論じているのは、証明または論証の前提とはどのようなものであり、それは結論とどのような関係にあるのか、ということです。たとえば、Frege が実際に使っている例ではありませんが、
Socrates は人間である。
人間はみな死ぬ。
故に Socrates は死ぬ。
という証明や、たとえば、これも Frege は使っていませんが、
1 = 2 だと仮定する。
私 Bertrand Russell とローマ法皇は、合わせて2人である。
仮定により、私 Russell とローマ法皇は、合わせて1人である。
というような証明 *18 に関し、その前提や結論について Frege は論じています。
以下の引用文内にある、この他の用語に対しては、いくつか簡単な解説を付け、それを引用文のあとに掲げますので、必要なかたは参照ください。
5. Frege の証言
それでは、EFQ/ECQ を Frege が認めるはずのないことがわかるドイツ語の原文とその邦訳を、次の文献から引用します。
・ Gottlob Frege Wissenschaftlicher Briefwechsel, hrsg., G. Gabriel et al., Felix Meiner, 1976, 邦訳、G. フレーゲ、『書簡集 付「日記」』、野本和幸編、勁草書房、2002年。
なお、ドイツ語原文にある註は省いて引用します。ドイツ語引用文中の「 [ ] 」は原文にあるものです。邦訳の「 [ ] 」、「( )」は、邦訳者によるものです。
Aus falschen Praemissen kann überhaupt nichts geschlossen werden. Ein blosser Gedanke, der nicht als wahr anerkannt ist, kann überhaupt nicht Praemissen sein. Erst nach[dem] ein Gedanke von mir als wahr anerkannt worden ist, kann er eine Praemisse für mich sein. Blosse Hypothesen können nicht als Praemissen gebraucht werden. Zwar kann ich, ohne die Wahrheit von A anerkannt zu haben, untersuchen, welche Folgerungen sich aus der Annahme, A sei wahr, ergeben; aber das Ergebnis wird dann die Bedingung wenn A wahr ist enthalten. Damit ist aber gesagt, dass A keine Praemisse ist; denn die wahren Praemissen kommen im Schlussurtheile nicht vor. Unter Umständen kann man durch eine Schlusskette ein Schlussurtheil gewinnen von der Form A, B, Γ erscheinen hierbei nicht als Praemissen des Schlussverfahrens, sondern als Bedingungen im Schlussurtheile. Man kann dieses von den Bedingungen befreien nur mittels der Praemissen ⊢ A, ⊢ B, ⊢ Γ und diese sind nun keine Hypothesen mehr, weil ihre Zeichen den Urtheilsstrich enthalten. *19偽なる前提からはそもそも何も推論できない。真であると承認されていないような単なる思想はそもそも前提 (Praemisse) とはなりえない。私によって真であると承認されて初めて、一つの思想は私にとって前提となりうるのである。単なる仮定 (Hypothesen) を前提として使用することはできない。たしかに、A が真であるという仮定 (Annahme) からどのような帰結が生じるかを、A の真理性を承認してしまうことなしに調べることは可能ではある。しかしその結果得られたものはその場合、A が真であるならばという条件を含むことになろう。だがそれは A は前提ではないということになる。というのも、真なる前提が帰結判断 [結論] (Schlussurtheil) の中に現われることはないからである。場合によっては、ある推論連鎖を通じて、
という形式をもつようなある帰結判断を獲得することはありうる。A, B, Γ はこの場合、推論手続きの前提として現われているのではなく、帰結判断の条件として現われている。この判断からそれらの条件を除去することは、前提 ⊢ A, ⊢ B, ⊢ Γ を用いることによってのみ可能となるのであるが、これらは、その記号が判断線を含んでいる以上、もはや仮定 (Hypothesen) ではないのである。 *20
6. Frege は EFQ/ECQ を認めなかったであろう。
さて、私たちは Frege が Ex Falso Quodlibet/Ex Contradictione Quodlibet (EFQ/ECQ) を推論規則として支持するのかどうかについて、疑問を持っていたのでした。そこで上の引用文を読んでみるとわかるのは、証明または論証の前提として、真である文や式しか Frege は認めようとしていない、ということです。彼にとって証明または論証の前提には、真である文または式がくるのであって、偽である文や、まして単なる仮定や仮説がくることは、正式/公式にはあり得ない、ということです。
したがって推論規則を前提の文に適用して結論を引き出そうとする場合、Frege の立場では、前提の文には真である文しか取ることはできません。言い方を少し変えると、推論規則が前提として取ることのできる文は、真な文だけです。偽な文や真でも偽でもない単なる仮定は取ることはできません。このため Frege の立場では、真な文を前提の文として取ることのできる推論規則しか、許容できないということです。
したがって、真とはされていない仮定を前提に取る推論規則は Frege には採用できません。Russell, Wittgenstein, Frege の研究者である Gregory Landini 先生も、
・ Gregory Landini Frege's Notations: What They Are and How They Mean, Palgrave Macmillan, 2012,
において、次のように語っておられます。(引用文中の [ ] は、引用者によるものです。)
Frege's [Grundgesetze] system did not adopt any provision for the modern technique of conditional proof - derivation under a hypothesis.
[...]
Frege's system does not embrace conditional proof as a primitive inference rule, [...] *24
加えて、偽である文を前提に取るような推論規則も、Frege には採用できない、ということになります。ここで EFQ/ECQ をふりかえってみると、この推論規則はその前提に偽である文か、または矛盾した文を取るのでした。矛盾した文はそれ全体で、通常、偽である文です。したがっていずれにしても、EFQ/ECQ は偽である文を前提に取りますし、それしか取ることができません。となると、Frege 先生に、「先生は EFQ/ECQ を推論規則としてお認めになられますか?」と尋ねれば、上の引用文からわかるように、「それは偽である思想を前提に取るが故に、そんなものは正当な推論規則としては認めるわけにはいかん!」と、秋霜烈日の如きお返事を賜ることになりそうです。ちょっと大げさですが...。
というわけで、しかし意外ですね。私たちの多くにとって EFQ/ECQ は、まぁよくわかっていないながらも、とりあえず普通に採用している規則だと思われますし、ましてや古典論理をはっきりと採用している人は、当然のごとく採用していると思われる規則ですが、その古典論理を採っている Frege が、にもかかわらず、本人の自論では EFQ/ECQ を採用するわけにはいかないというのですから、何だか意外です。
とはいえ、先ほど引用したばかりの文に続いて、Landini 先生は少し気になることを記しておられます。直前の引用文の後半をもう一度引きながら、その続きを引用します。
Frege's system does not embrace conditional proof as a primitive inference rule, although it is certainly a derived inference rule of his system [...] *25
とすると、真とは限らない文を仮定として立てて、結論を導く規則を derivable rule としてなら Frege は許容すると Landini 先生はお考えなのでしょうか。実際、今引用した文の後で、Frege はその規則を許容すると先生は主張されています。しかし本当に Frege はそれを許容するのだろうか?
しかも先生は、理論上、Frege の Grundgesetze 体系では、真ではない式に判断線を付けることができ、かつ実際 Frege は Grundgesetze で何度もそうしている、とも主張されています *26 。
う~む、このあたり、私自身、再考してみる必要があると感じます。
7. まとめ
最後に、今日の話を手短にまとめます。
Frege は推論規則 Ex Falso Quodlibet/Ex Contradictione Quodlibet (EFQ/ECQ) を認めただろうか?
この規則 EFQ/ECQ は、その前提に偽である文を取ります。ところで Frege は、その前提に偽である文を取る推論規則を認めません。
故に、Frege は EFQ/ECQ を認めません。
ところで、Frege は古典論理を採用しています。古典論理を採用している者は、EFQ/ECQ を採用します。したがって、Frege も EFQ/ECQ を採用しているはずです。
が、しかし彼は、今言ったとおり、その規則を採用するつもりはありません。これは意外です。
以上です。これが本日述べようとしていた「ささいなことながら、個人的に意外に思ったこと」でした。
今回の話の中に、誤解や無理解や勘違い、誤字や脱字や衍字が含まれていましたら、お詫び致します。どうかお許しください。
*1:以下で述べられることは確かにささいなことですが、掘り下げると重要な事柄につながってくると思われます。何がそこで述べられているのかというと、ある論理体系で推論規則が derivable であるとか admissible であるということにつながる話題です。たとえばある論理体系において選言三段論法 (この規則は後の註12で説明します) が original な推論規則でもなければ derivable な規則でもないが、しかし admissible な規則であることが証明されている場合、そのことの哲学的な point はどこにあるのか、そのようなことが検討されたことがありますが (Anderson and Belnap)、私としてはその選言三段論法に関係のある推論規則 Modus Ponens (略して MP, 詳細後述) が、ある論理体系において original な規則でもなければ derivable でもなく、しかし admissible である場合、そのような規則にいかなる哲学的 point があるのか、あるいはないのかが、興味深く感じられます。ところで人間の主要な特徴の一つは、それが理性を持った動物であるという点です (感情も大切ですが)。そして理性の特徴は推論能力にあると思われます。その推論の典型的な pattern は「p である。p ならば q である。故に q である」という推論規則 MP だと思われます。つまり MP は理性の主要な特徴を成し、理性が人間の主要な特徴を成すならば、MP は人間の主要な特徴を成すだろう、ということです (動物も MP を駆使しているかもしれませんが。ワンワンだって選言三段論法を駆使していると古代ギリシアの時代から言われていることですし。J.アナス他、『古代懐疑主義入門』、金山弥平訳、岩波文庫、岩波書店、2015年、102-103、128-130ページ、当 blog 2015年9月27日)。そしてこの MP について、derivability や admissibility などの概念を通じて、何か興味深い事柄が判明するならば、それは人間の興味深い事柄が判明したことになるでしょう。故に、MP や MP 以外の、人間が有すると思われる重要な推論規則について、それが derivable であるとか admissible であるなどなどを検討した話題は、おそらくですが、重要な事柄に至り着く可能性があると思われます (ずいぶん大風呂敷を広げたものですが)。ある論理体系で推論規則が derivable である、admissible であるということについて、教科書的な説明は次を参照ください。J. von Plato, Elements of Logical Reasoning, Cambridge University Press, 2013, p. 47, 戸次大介、『数理論理学』、東京大学出版会、2012年、202ページ。ただし本日の話には、derivable であるとか admissible であるということに関しては、それらについて私の理解がまだあやふやなところがありますので、ほとんど出てきません。どうかご了承ください。いずれにしましても私自身は、先ほど述べたみたいに、大風呂敷を広げて威勢よく自論を展開するだけの力はありませんので、ここではささいなことを記すにとどめます。なお、その「ささいなこと」は、以下本文に掲げる Franks 論文を読めば誰にでもすぐ気が付くことですので、本日の日記には、私の original な主張は何もございません。
*2:以下、言語表現が使用されているのか、言及されているのか、その区別については、特には明示しません。常識的にわかると思いますので。
*3:この規則については、たとえば、前原昭二、『記号論理入門』、日本評論社、1967年、37-38ページを参照。この本の2005年新装版も同ページ。1967年版も2005年新装版も、本文のページに変更はないので、以下、新装版のページ数は省きます。
*4:私も Frege については詳しくありません。
*5:Gottlob Frege, Begriffsschrift und andere Aufsätze, 2. Auflage, hrsg., I. Angelelli, Georg Olms, 1964, SS. 7-8, 邦訳、フレーゲ、『概念記法』、藤村龍雄訳、勁草書房、1999年、18-19ページ、Gottlob Frege, Grundgesetze der Arithmetik I/II, Georg Olms, 1998, S. 25, 邦訳、フレーゲ、『算術の基本法則』、野本和幸他訳、勁草書房、2000年、89ページ。
*6:EFQ/ECQ を正しい推論規則としては認めないという立場もあります。なぜ認めないのかという話をし出すと大幅に脱線して行きますので、今はこのことには深入りしません。EFQ/ECQ を認めない人たちには relevance/relevant logicians, paraconsistent logicians, dialehtheists がいます。
*8:前原、『記号論理入門』、45, 53, 56ページ。この paragraph の話は、左記前原先生の著作該当ページに出てくる「起り得べからざること」という言い回しを hint に私のほうで考えてみたものです。前原先生が、この paragraph で述べられていることと同じことを左記の該当ページで述べておられるわけではありません。先生の著作から hint をもらいましたので、ここにその該当ページを一応明記しておきます。
*9:このあとの証明については、いくつかの文献で見られますが、たとえば次を参照ください。古いところでは、C. I. Lewis and C. H. Langford, Symbolic Logic, Dover Publications, 2nd edition, 1959, p. 250, 新しい教科書では、G. Priest, An Introduction to Non-Classical Logic, 2nd ed., Cambridge University Press, 2008, p. 76, 日本語で読める文献には、G. E. ヒューズ、M. J. クレスウェル、『様相論理入門』、三浦聰他訳、恒星社厚生閣、1981年、330-333ページ、カール R. ポパー、『推測と反駁』、藤本隆志他訳、法政大学出版局、1980年、587-591ページ、林晋、『数理論理学』、コロナ社、1989年、25ページ。
*10:この式は「p かつ p でないならば、q である」と読まれます。
*11:この証明で使われる推論規則は初歩的なものばかりですが、ご存じでないかたは、前原、『記号論理入門』、「第2章 演繹」など、論理学の入門書をご覧ください。
*12:選言三段論法 (disjunctive syllogism)。「(p または q) かつ p でないならば、q」。この式の具体例としては、たとえば「太郎は家にいるか、または学校におり、かつ彼が家にいないならば、学校にいる」というものが挙げられます。
*13:ただし、先ほどの註6でも触れたように、EFQ/ECQ を正しい規則としては認めないという立場もあります。一応、標準的な見解 (classical logic) では、EFQ/ECQ は正しいものと考えられています。
*14:ちなみに、矛盾が人々から嫌われ拒否される論理的な理由は、EFQ/ECQ が成り立つことにあります。つまり矛盾からは、この EFQ/ECQ によって何でも引き出すことができ、その結果、何でも正しいことになってしまうので、論理的に言って、矛盾は認められない、というわけです。
*15:野本和幸、『フレーゲ哲学の全貌』、勁草書房、2012年、223ページ。
*17:その他に、似たような証言をどの文献で Frege が残しているのかについては、今日の日記冒頭で掲げた論文 Franks, ''The Context of Inference,'' pp. 369-370 を参照。
*18: Russell = the Pope というこの論証については、林晋、『数理論理学』、25ページ、脚注†、または当 blog, 2014年2月23日、''Russell Proved that He was Identical with the Pope'' をご覧ください。なお、2018年12月31日までのこの blog の記事は、はてなダイアリーで書き、それをすべてこちらのはてなブログに2019年になってから inport しました。その際、体裁の崩れや文字化けが多数発生しています。記事が読みにくくなっていましたら大変すみません。ちなみに、今本文で挙げた二つの証明のうち、最初の Socrates の例では、前提の文がどれも実際に真であること、そして二つ目の Russell = the Pope の例では、前提の文に仮定および偽である文が含まれていることが、このあと本文で関係してきます。
*19:Frege, Wissenschaftlicher Briefwechsel, „Frege an Jourdain, ohne Datum‟, S. 118.
*20:フレーゲ、『書簡集』、中川大、長谷川吉昌訳、フレーゲよりジャーデイン宛 (日付なし)、200ページ。
*21:ここで私が書いていることについては、Frege の論文 „Gedanke‟ を読まれるか、野本和幸先生の著書をひも解かれましたら、大体この種のことが書いてあると思います。以下の説明は、私のほうでやさしく、わかりやすく言い直しています。上の引用文の内容を大よそ理解するだけであれば、あまり厳密な用語説明は不要だと思いますので、緩やかな説明をしています。どうかご容赦ください。
*22:実際は、その思想は偽です。というのも、漱石は1900-2年頃、鴎外は1880年代に留学しているようなので。
*23:詳しい説明は、当 blog, 2012年7月15日、 Entry 'Why Did Frege Need Judgement Strokes and Horizontal Strokes in his Grundgesetze der Arithmetik?' を参照ください。
*24:Landini, p. 33.
*25:Ibid.
*26:Landini, op.cit., pp. 31-33.