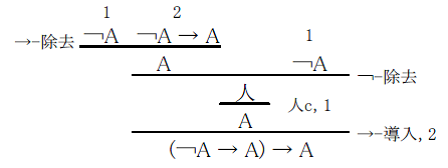今日は consequentia mirabilis と reductio ad absurdum (背理法/帰謬法) の関係について記します。一般に両者には対応関係があるとされていますが*1、ある先生のお話によると、前者は後者の基礎、基本、根拠のようなものになっているとのことです。ただ、私自身は本当にそうなのか、疑問に感じています。少し詳しく検討してみると、前者は後者の基礎となっているのか、私にはわからなくなってきました。そこで今日は両者の関係を少し詳らかにしておこうと思います。(ただし、少しだけです…。)
なお、両者の関係を明らかにすることは、[ある先生のご意見が正しいとすると(2016年1月5日追記)] 場合によっては重要です。おそらく多くの方が両者の関係を問うことに、ただちには意義を見出さないかもしれませんが、それでも場合によってはとても重要であると考えます。どうして重要なのかについては、申し訳ありませんが今日はお話しできません。可能ならばまた日を改めてご説明致します。実際にはその説明は簡単に済むのですが、私には時間がないことと、話が分かれて行ってしまうので、本日のお話にはその説明は含めません。両者の関係の重要性に関し、意義を感じておられない方は、以下の話にあまり興味を持つことができないかもしれませんが、どうかお許しください。すみません。
また、以下の話は私の感じている疑問を提示するだけです。疑問を提示しながら誰かに反論を加えるものではございません。少なくともそのような意図はないつもりです。疑問を提示しているだけ、というのは、「A は B なのだろうか? う〜む、よくわからないです…」と言っているだけ、ということです。決して「A は B なのか? いや、断じて A は B なんかではない!」と主張しようとしているのではない、ということです。具体的には「consequentia mirabilis は reductio ad absurdum の基本形なのだろうか?」という疑問に関して以下で少し詳しい話をします(「基本形」のいみが差し当たり何であるとしても)。この疑問に対して、積極的に yes であるとも no であるもと主張しないつもりです。ただ、どちらかというと、no という気持ちに私は傾いていますが…。あるいは、私の述べる疑問は、私が何もわかっていないから疑問に感じているだけなのかもしれません。そのようでしたらすみません。もっと勉強致します。
加えて、以下では論理学に絡んだ話が出てきますが、私は論理学に関して無知です。苦手意識を強く持っており、よくわからないことが多いので、そんな論理学の話をしている以下の記述には、論理学の初歩的な話しかしていないとはいえ、大きな間違いが含まれている可能性が非常に高いです。重要な点を抜かしてしまっている可能性があります。見当違いなことを述べているかもしれません。ですので、正しいことを述べているものとは初めから思い込まずに、お読みいただける場合は、批判的な姿勢を失わないようにしてください。あらかじめ含まれているはずの誤りに対し、ここでお詫び申し上げます。
目次
1. 「Consequentia mirabilis は reductio ad absurdum の基本形である。」
2. Consequentia mirabilis とは何か?
3. 背理法、consequentia mirabilis, 排中律、2重否定除去則の関係
3.1. 背理法、排中律、2重否定除去則の関係
3.2. 背理法と consequentia mirabilis の関係
4. 単独の式としての consequentia mirabilis と背理法の関係
5. Consequentia mirabilis と背理法原理との関係
5.1. 背理法原理の仮定から consequentia mirabilis への証明
5.2. Consequentia mirabilis の仮定から背理法原理への証明
6. おわりに
補遺
Consequentia mirabilis 第二型の仮定から、背理法原理第二型への証明
背理法原理第二型の仮定から、consequentia mirabilis 第二型への証明
1. 「Consequentia mirabilis は reductio ad absurdum の基本形である。」
以下に出てくる A, B などは、文または式を表します。これらの表現と、その他の論理記号などに言及する際、しばしば引用符を省き、言語表現の使用と言及の区別を逐一明示することは、たびたび略します。
さて、
- Stephen Read Thinking About Logic: An Introduction to the Philosophy of Logic, Oxford University Press, OPUS Series, 1995,
の p. 162 では、背理法/帰謬法 (reductio ad absurdum) の基本形 (basic form) は consequentia mirabilis である、と書いてあります。
原文を引用してみると、背理法について、
Its basic form is that of consequentia mirabilis, 'if A then not-A; so not-A'.
とあります。ここで言われている 'basic form' とは何でしょうか。著者の Read 先生は何も説明されておられないので、詳細はわかりません。
上記書籍巻末の glossary の p. 251 では、背理法を次のような形式を持った式であると記しています。
'if A then both B and not-B, so not-A' and, in classical but not intuitionistic logic, 'if not-A then both B and not-B, so A'.
そして、その glossary の p. 248 では、consequentia mirabilis を次のような形式を持った式だと記しています。
'if A then not-A, so not-A' and 'if not-A then A, so A'.
上に示したような consequentia mirabilis が、背理法と密接な関係にあることを示唆している由緒正しい文献がまた別にあります。 Principia Mathematica です。
- Alfred North Whitehead and Bertrand Russell Principia Mathematica to *56, Cambridge University Press, Cambridge Mathematical Library, 1997, 1st ed. published in 1910, 2nd ed. published in 1927,
の p. 100 の proposition *2・01 は
-
- ⊢: p ⊃ 〜p .⊃. 〜p
であり、
This proposition states that, if p implies its own falsehood, then p is false. It is called the ''principle of the reductio ad absurdum,'' […]
と述べられています。
また、上記 Principia, p. 103 の proposition *2・18 は
-
- ⊢: 〜p ⊃ p .⊃. p
であり、その pp. 103-104 にかけて
This is the complement of the principle of the reductio ad absurdum. It states that a proposition which follows from the hypothesis of its own falsehood is true.
とあります。
ただし、これら *2・01, *2・18 が提示されているところでは、なぜこれらの propositions が the principle of the reductio ad absurdum と、その complement と言えるのかに関しては、何も説明がありません。
改めて、Read 先生の文を、一部並べてみましょう。形式化された式も当方で付加します。
Consequentia mirabilis
-
- If not-A then A, so A. (¬A → A) → A
-
- If not-A then both B and not-B, so A. (¬A → (B ∧ ¬B)) → A
矛盾 B ∧ ¬B は、しばしば 人 で表されます。そこで、背理法を表した直前の式に関し、人 を使って書き直すと、
-
- (¬A → 人) → A
となります。
今一度、consequentia mirabilis と背理法を、この順で並べましょう。
-
- (¬A → A) → A
- (¬A → 人) → A
この並びから想像するに、Read 先生がこれらの式の前者である consequentia mirabilis を、後者である背理法の基本形 (basic form) と呼ぶのは、前者の二番目に現われている A を、人 に代えたものが後者になるからではないでしょうか。つまり、前者の二番目の A を特殊化した 人 に代えたものが後者になるということ、あるいは逆に、後者の 人 を一般化して A に代えたものが前者になるということではないでしょうか。 これが先生によって「基本形」と呼ばれるゆえんではないでしょうか。
もちろん、Read 先生ご自身は何も詳細を述べておられないので、確実なことはわかりません。先生にとって基本形とは何であるかについては、当座のところ判断を保留します。しかしいずれにせよ、背理法の基本にあるものは consequentia mirabilis であるということ、背理法を支えているのが consequentia mirabilis であるということ、背理法を正当化し、その正しさを保証しているのが consequentia mirabilis であるということ、何かこの種のことを Read 先生はお考えであろうと想像されます。
しかし、そのような先生のご想像は正しいでしょうか。つまり、背理法を正当化しているのは consequentia mirabilis なのでしょうか。
2. Consequentia mirabilis とは何か?
ところで、背理法はみな知っていることだからまずよいとして*2、consequentia mirabilis とは正確に言って何なのでしょうか。
Consequentia mirabilis という名前は、おそらく16世紀後半頃から言われ始めた言葉です*3。Consequentia mirabilis というこの言葉が表す推論形式の起源を探してさかのぼっていくと、その淵源の一つに Aristotle の文章があります*4。では、Aristotle は何を consequentia mirabilis としていたのでしょうか。次の文献を参考にしてみます。
- William Kneale ''Aristotle and the Consequentia Mirabilis,'' in: The Journal of Hellenic Studies, vol. 77, Part 1, 1957.
この論文によると、Aristotle は次のように述べたと言われています。
'If we ought to philosophise, then we ought to philosophise; and if we ought not to philosophise, then we ought to philosophise (i.e. in order to justify this view); in any case, therefore, we ought to philosophise'.*5
Kneale 先生によると、これが哲学の文献に史上初めて現れた、後に consequentia mirabilis と呼ばれる推論の pattern です*6。今の引用文を形式化してみましょう。すると以下のようになります*7。これを論証 (iv) と呼びましょう。(iv) と呼ぶのは、Kneale 論文で、この論証に (iv) という名が付いているからです。
If P then P
If not-P then P
But either P or not-P
∴ P
この形式化された論証において、一行目の 'If P then P' は一般に自明であって成り立って当然であり、三行目の 'But either P or not-P' も通常は成り立つものとされる排中律に他なりません。そこでこれら二つのわかり切った式を省けば、上記の論証は以下のようになります*8。論証 (v) と呼びましょう。(v) と呼ぶのも Kneale 論文に依ります。
If not-P then P
∴ P
これが consequentia mirabilis を論証の形にしたものです。式に書き直せば、
If (if not-P then P) then P
となります*9。これを式 (viii) と呼びます。こう呼ぶ理由も Kneale 論文にあります。
また、Kneale 先生によると、次も consequentia mirabilis の variant であるとしています。これは論証 (vii) の名を持っています*10。
If not-P then P
If not-P then not-P
But not both P and not-P
∴ not-not-P
∴P
ここでも、上記論証 (iv) の場合と同様、この論証を構成している式の一部は自明であり、便宜的に省くことができます。さしあたり省くことが可能なのは2行目の 'If not-P then not-P' と3行目の 'But not both P and not-P' と4行目の 'not-not-P' です。3行目は伝統的に矛盾律 (the Law of Non-Contradiction) と呼ばれてきたものです。4行目の2重否定は一般に肯定と考えられるので、5行目の 'P' があれば間に合うから省かれます。ちなみに4行目から5行目への推論の移行は、2重否定の除去の規則 (Not-not-P, ∴P)*11 によって正当化されます。こうして2, 3, 4行目をすべて省けば、この論証 (vii) は先ほどの論証 (v)
If not-P then P
∴ P
と同じになることがわかります。
以上により、Kneale 先生の見る通り、歴史的に言って、consequentia mirabilis とは、上記の論証 (v) または式 (viii) のことだとしましょう。そしてこれらの論証 (v) と式 (viii) は、正確には論証 (iv) または (vii) の省略形に過ぎず、(v) と (viii) の正しさは、それらを full で書いた論証 (iv) または (vii) にあるとしましょう。つまり、consequentia mirabilis の省略形 (v), (viii) の正しさは、それらを full で書いた (iv), (vii) によって、いわば支えられている、ということです。(iv), (vii) という、いわば background をもとに (v), (viii) の正しさが保証されている、ということです。そこで問題となるのが full で書かれた論証 (iv) の三行目 'But either P or not-P', つまり排中律と、論証 (vii) の4行目から5行目への推論の移行を正当化する 'not-not-P, ∴P', つまり2重否定の除去の法則です。これら排中律と2重否定除去則が、どのように問題となるのかは、この後おいおい明らかになるでしょう。
3. 背理法、consequentia mirabilis, 排中律、2重否定除去則の関係
さて、ここで思い出しておきたいのは、Read 先生が consequentia mirabilis こそ、背理法の基本形だとしていたことです。これについて、ここまでの話に基づき言い足すならば、背理法が正当化されるのは、その基本形である consequentia mirabilis によってであり、そして今、Kneale 論文の中で、consequentia mirabilis を正当化しているものとして、排中律と2重否定除去則が出てきたということです。では、もう少し詳しくは、背理法と consequentia mirabilis と排中律、2重否定除去則の、これら四者の関係は、いかなるものでしょうか。
とりあえず、まずはよく知られている背理法と排中律の関係はいかなるものでしょうか。両者の関係に関し、次の文献を参考にしてみましょう。
この本から引用してみます。前原先生の本からの引用に関しては、その引用文中の '< >', '( )', '[ ]' は原文にあるものであり、太字も原文通りで、'〔 〕' は引用者によるものです。なお、引用文中の '人' は矛盾を表します。
§8. <排中律> について
排中律: A ∨ ¬A
1. 排中律 (tertium non datur) もまた、われわれの日常言語感覚からすれば、任意の命題 A に対してつねに成立するものと考えられます。そして、それは、本質的な意味での間接証明 [すなわち背理法] の基礎を与えているものです。
背理法 [または帰謬法 (きびゅうほう)] というのは、A という命題を証明するために、A の否定 ¬A を仮定して矛盾を導いてみせる、という証明法です。すなわち、¬A → 人を証明すれば、それで A の証明が得られたことになる、という考え方です。*12
この引用文からすると、背理法とは、式で表わせば、以下のようになるでしょう。
背理法の原理 Formula Version
-
- (¬A → 人) → A
そして前原先生は直前の引用文に続けて次のように述べておられます。
¬A → 人 というのは A の2重否定
¬¬Aのことにほかなりませんから 〔…〕、背理法の原理は2重否定の除去の法則
¬¬A → Aによって表わされているものであります。*13
「¬A → 人 というのは A の2重否定 ¬¬A のことにほかなりません」とは、以下のことを言います。まず、
-
- ¬A → (A → 人) かつ (A → 人) → ¬A
が証明できます。証明図で示しましょう*14。最初に ¬A → (A → 人) です。
続いて、(A → 人) → ¬A です。
よって、¬A → (A → 人) かつ (A → 人) → ¬A ですから、'≡' を同値記号、必要十分条件の記号とすれば、
-
- ¬A ≡ (A → 人)
が証明可能であって、この式の A に ¬A を代入すれば、
-
- ¬¬A ≡ (¬A → 人)
が証明されることに依ります。
したがって、背理法の原理
-
- (¬A → 人) → A
の ¬A → 人 の部分を ¬¬A に置き換えてよく、そのようにしてやれば、背理法の原理は2重否定の除去の法則
-
- ¬¬A → A
そのものとなります。
ところで、排中律を仮定してやれば、2重否定除去の法則を引き出すことができます。かつ逆に、2重否定除去の法則を仮定してやれば、排中律を引き出すことができます。まず、排中律の仮定から2重否定除去の証明図を記し、続いて2重否定除去の仮定から排中律の証明図を記します*15。
したがって、先ほど見たように、背理法の原理から2重否定除去の法則を出すことができ、そして今述べたように、2重否定除去の法則から排中律を出すことができるので、背理法の原理から排中律を出すことができます。かつ逆に、排中律から2重否定除去の法則を、2重否定除去の法則から背理法の原理を、引き出すことができるので、排中律から背理法の原理を引き出すことができます。矢印を使って簡潔に定式化すると、
です。
これは言い換えれば、背理法の原理と排中律とは、同じことの別々の姿である、とも言い得るし、背理法の原理と2重否定除去則とは、同じことの別々の姿である、とも言い得ます。これも定式化してみれば、
です。
ここからしてさらには、背理法原理、排中律、2重否定除去則という三者が、結局いずれも同じことの別の現れと見なすことができます。やはり定式化してみれば、
です*16。
3.2. 背理法と consequentia mirabilis の関係
ここで、Kneale 論文による consequentia mirabilis の説明を思い出しましょう。そこにおいて consequentia mirabilis の full version は論証 (iv) と (vii) でした。それぞれをこの順で再度掲示しましょう。
If P then P
If not-P then P
But either P or not-P
∴ P
If not-P then P
If not-P then not-P
But not both P and not-P
∴ not-not-P
∴P
改めてこれらの論証をよく見てみましょう。前者の (iv) では3行目に排中律が含まれています。後者の (vii) では4行目から5行目への移行に際し、2重否定除去則が使われています。そしてこれら排中律と2重否定除去則は、ともに背理法原理の別の姿でした。すると、ここから理解できるのは、 consequentia mirabilis を支えている論証には、背理法原理が使われているということであり、consequentia mirabilis は背理法原理に依存しており、背理法原理によって正当化されている、ということです。ちなみに Kneale 論文の p. 63 では、上記論証 (vii) において、その4行目 not-not-P から5行目 p への移行が許されること (the law of double nagation) により、consequentia mirabilis が正当化されているのだ、と述べられています。つまり2重否定除去則/2重否定除去の法則は、consequentia mirabilis を正当化する役割を負っているというのです。
振り返ってみると、Read 先生は背理法の「基本形」を consequentia mirabilis であるとしておられました。「A の基本形は B である」ということで、A は B に依存しており、A は B によって正当化されることをいみするならば、consequentia mirabilis と背理法の関係は、ここまで私が述べてきたことからして、Read 先生のおっしゃることと逆になっているのではないでしょうか? 背理法の「基本形」は consequentia mirabilis なのではなく、逆に、consequentia mirabilis の「基本形」が背理法なのではないでしょうか?
この疑問に対し、次のような意見があるでしょう。つまり、「Consequentia mirabilis は、論証である (iv), (vii) なのではなく、単なる式である上記の (viii) If (if not-P then P) then P にすぎないのであって、この式自身には背理法原理も排中律も2重否定除去則も現れてはいない。だから、この式自身を consequentia mirabilis と見ればいいのである。実際に、通常、'consequentia mirabilis' と言われるものは、何らかの論証を指すのではなく、ただの式を指しているだけなのだ。論証など持ち出すことが、そもそもの間違いなのである」と。
4. 単独の式としての consequentia mirabilis と背理法の関係
では、今の指摘に従って、consequentia mirabilis を単独の式 (viii) If (if not-P then P) then P にすぎないものとしてみましょう。さて、そうすると、この式はなぜ正しいと言えるのでしょうか? なぜ成り立つと言えるのでしょうか?
この式を公理のように初めから正しいものと約束するのでないならば、この式の正しさは証明されねばならないでしょう。でしたら、その証明はどのようなものになるでしょうか? 実際にその証明を見てみましょう。次が考えられる証明です。
この証明図の一番下にある式 consequentia mirabilis を証明するのに何が使われているでしょうか? 証明図の下の方に (人c) という推論が使われているのがわかります。これは「1」という番号の付いた '¬A' を仮定として立てた後、矛盾 '人' が出てきたら、'A' をただちに結論してよい、とする推論規則です*17。
これはまさしく背理法に他なりません。このように、consequentia mirabilis の正しさは、背理法によって証明されているのです。Consequentia mirabilis が背理法を正当化しているのではなく、逆に背理法が consequentia mirabilis を正当化しているのです。これは Read 先生の見解に反します。
5. Consequentia mirabilis と背理法原理との関係
ここまでの話をまとめましょう。まず、論証としての consequentia mirabilis の full version では排中律と2重否定除去則が含まれていることを見ました。そして排中律と2重否定除去則は背理法原理の別の姿であることを確認しました。したがって、consequentia mirabilis の full version からすると、consequentia mirabilis が背理法を正当化しているのではなく、逆に背理法の原理によって consequentia mirabilis が正当化されているのだ、ということを確かめました。しかし、consequentia mirabilis とは、論証の形で書かれた full version ではなく、単独の式として理解すべきであるとの指摘により、改めて consequentia mirabilis を単独の式として捉え直してみました。その結果、単独の式としての consequentia mirabilis の正しさも背理法によって保証されていることを把握しました。Consequentia mirabilis の full version でも、単独の式でも、それは背理法によって正当化されているのであり、背理法が consequentia mirabilis によって正当化されているのではないことがわかりました。よって、背理法の基本形が consequentia mirabilis であるとする Read 先生の見解は間違っている、と結論できるでしょうか。そう結論する前に、少なくともあと一つ、検討しておかなければならないことがあります。
Section 1. の末尾、あるいは section. 2 の直前に、次のように記していました。
今一度、consequentia mirabilis と背理法を、この順で並べましょう。
- (¬A → A) → A
- (¬A → 人) → A
この並びから想像するに、Read 先生がこれらの式の前者である consequentia mirabilis を、後者である背理法の基本形 (basic form) と呼ぶのは、前者の二番目に現われている A を、人 に代えたものが後者になるからではないでしょうか。つまり、前者の二番目の A を特殊化した 人 に代えたものが後者になるということ、あるいは逆に、後者の 人 を一般化して A に代えたものが前者になるということではないでしょうか。 これが先生によって「基本形」と呼ばれるゆえんではないでしょうか。
この引用文で述べていることは、引用文中に現われている二つの式のうち、前者 consequentia mirabilis の特殊例が後者の背理法原理になっているということ、あるいは後者の背理法原理を一般化したものが前者の consequentia mirabilis になっているということです。
ここでは consequentia mirabilis と背理法原理との関係を、特殊/一般との関係として述べています。そして上記引用文の後、本日の日記本文中では、consequentia mirabilis の full version に背理法原理が含まれていること、その単独の式の version も背理法によって正当化されることを見ました。これら以外に consequentia mirabilis と背理法との関係で検討しておかなければならないことは、両者のもっと直接的な関係です。すなわち、Read 先生が consequentia mirabilis を背理法の基本形であると述べている際に、先生の念頭にあったのは、両者の特殊/一般的な関係ではなく、さらには consequentia mirabilis の full version や単独の式の version を支えている背理法との関係でもなく、consequentia mirabilis (¬A → A) → A から背理法原理 (¬A → 人) → A が導かれるということ、かつ/または、背理法原理から consequentia mirabilis が導かれるということではなかったのか、ということです。つまり問われるべき問題は、consequentia mirabilis を仮定すれば、背理法原理が証明できるのだろうか、かつ/または、背理法原理を仮定すれば、consequentia mirabilis を証明することができるのだろうか、ということです。その答えを述べるならば、「両方とも証明できる」です。まずは後者に関し、背理法原理を仮定することで、consequentia mirabilis が証明できることを示し、続いて前者に関し、consequentia mirabilis を仮定することで背理法原理が証明できることを示しましょう。
5.1. 背理法原理の仮定から consequentia mirabilis への証明
背理法原理の仮定から consequentia mirabilis への証明を、端的に図を用いて示すならば、以下の通りです。
各推論の step で、どのような推論規則が使われているか、ご確認ください。今回の話題において、特に問題となる規則は使われていないことがわかります。
5.2. Consequentia mirabilis の仮定から背理法原理への証明
次に、肝心の consequentia mirabilis から背理法原理への証明を、やはりここでも端的に図にして示しましょう。
使用されている推論規則をご覧ください。図の下の方で (人c) が使われているのが見えます。これによりわかることは、consequentia mirabilis から背理法原理が証明できるとしても、それは背理法の助けを借りてのことなのだ、ということです。Consequentia mirabilis から背理法原理が証明できるとしても、それを保証しているのは背理法という規則によってなのだ、ということです。背理法という規則によってこそ、consequentia mirabilis から背理法原理への証明が正当化されるのです。そして consequentia mirabilis が背理法の基本形だという Read 先生の主張の内実が、前者から後者が証明できるとすることにあったのならば、その時には実は背理法の規則が使われてしまっているのだ、ということです。だとすると、Read 先生の主張には循環が見られる、あるいは先生は論点先取の虚偽を犯してしまっていると言えるのではないでしょうか。
6. おわりに
ここまでを非常に手短にまとめます。
Read 先生は、consequentia mirabilis によって背理法が正当化されるとお考えのようでした。しかし、consequentia mirabilis を論証の形態で考えた場合、その論証を構成する式の一つには、背理法原理に deductively equivalent な排中律、あるいは2重否定除去の法則が出てきていることがわかりました。そしてこれら排中律、2重否定除去の法則によって、その論証の正当性が維持されるので、Read 先生のお考えとは逆に、consequentia mirabilis が背理法を正当化しているのではなく、背理法原理の別の姿である排中律、2重否定除去の法則こそが consequentia mirabilis を正当化しているのを見ました。
また、consequentia mirabilis を単独の式と考えた場合にも、consequentia mirabilis が背理法を正当化しているのではなく、その逆に、背理法によってこそ、consequentia mirabilis の正当性が保証されていることを見ました。
さらに、単独の式としての consequentia mirabilis と背理法原理の関係を考えた場合、前者から後者への、かつ後者から前者への証明が存在するのですが、仮に Read 先生が consequentia mirabilis と背理法の関係を、前者から背理法原理への証明が存在することをもって、consequentia mirabilis が背理法原理を正当化しているのだとお考えであったとするならば、consequentia mirabilis から背理法原理への証明中にも背理法が使用されていることからして、その場合、背理法によって consequentia mirabilis が正当化されているので、consequentia mirabilis による背理法原理の正当化が存在するとは言えず、Read 先生のお考えとは事態が逆であることを見ました。
以上により、consequentia mirabilis が背理法を正当化していると Read 先生はお考えであったようなのですが、実際には背理法が consequentia mirabilis を正当化しているというのが実態だと思われ、Read 先生のお考えは間違っているのではないかと推測されます。
しかし、本当にお間違えなのかどうか、私は判断を保留します。私は論理学に疎く、何か大切なことを見落としているのかもしれません。そのため、先生を誤解しているのかもしれません。したがって、先生はお間違えになっておられると断言することは致しません。間違っているのは私の方かもしれません。
はたして先生が正しいのか、私が正しいのか、今後、可能ならば自分の中ではっきりとさせていきたいと思います。というのも、本項目の一番最初でわずかに示唆しましたが、Read 先生の言う通り、consequentia mirabilis が背理法を正当化しており、前者が後者を支えているとするならば、とても重大な問題がそこには生じるからです。どのような問題が生じるのかは、Read 先生が明瞭に指摘しておられます。この重要な問題については、できることならば、後日、本日記で説明したいと思います。
補遺
今回の記述では、単独の式としての consequentia mirabilis を
-
- (¬A → A) → A
と理解し、これに対応する背理法原理を
-
- (¬A → 人) → A
と理解して話を進めてきましたが、section 1. の一番初めに出てくる Read 先生の引用文を見ていただいてもおわかりの通り、先生は
-
- (A → ¬A) → ¬A
も consequentia mirabilis を表す式であるとお考えであり、この式に対応する背理法原理を、先生は
-
- (A → 人) → ¬A
ともお考えであったことが、section 1. の二番目に出てくる引用文から把握できます。
そこで、あとの二者の式の一方から他方が、かつ他方から一方が証明できるのかを考えてみましょう。あとの二者のうち、前者を consequentia mirabilis 第二型*18、後者を背理法原理第二型と呼ぶことにしましょう*19。さて、実際考えてみればわかりますが、consequentia mirabilis 第二型を仮定すれば、背理法原理第二型を証明することができ、かつ逆も証明できます。それを念のために下に掲げましょう。
Consequentia mirabilis 第二型の仮定から、背理法原理第二型への証明
背理法原理第二型の仮定から、consequentia mirabilis 第二型への証明
上記二つの証明図の、各推論 step で使われている推論規則には、どこにも (人c) は使われていません。このように、これらの証明図では特に今回問題となりそうな規則は使われていません。この点は、いささか興味深いことですが、ここまで、話も長くなっていることなので、これ以上の考察は一旦中断することに致します。
PS
念のために最後に一言。Angelelli 先生の ''Two Attempts to Disenchant the ''Consequentia Mirabilis'''' はとても参考になりましたが、私は Angelelli 先生とは立場を異にします。先生によると、consequentia mirabilis は背理法と無関係だ、とのことですが、上で私が述べたことは、先生とは反対に、それら二つは密接に関係しているということであり、明示的にではないものの、きっと後者が前者を正当化しているのだろう、ということが私の現在の立場です。しかし私の方が間違えていましたらすみません。謝ります。
以上で終わります。誤解や無理解や勘違い、誤字や脱字などが含まれているようでしたら、すみません。'consequentia mirabilis' という語をコピペではなく、全部自分でその都度サクサク手打ちして行きましたので、どれか打ち損じがあるかもしれません。いちいち check していませんので、誤記しておりましたらごめんなさい。また、初めにも少し申しましたが、私は論理学をよく知りませんので、ここまでお読みいただいた方は、絶対に上の私の話をそのまま鵜呑みにしないようにしてください。絶対どこか間違っています。一つ一つ慎重に読み返してください。そうすれば読者の方も間違いに足をすくわれずにすみますし、批判的に分析する能力も向上すると思います。誤りに対して、再度お詫び申し上げます。また勉強に精進致します。
*1:戸次大介、『数理論理学』、東京大学出版会、2012年、158ページ。
*2:とはいえ背理法と、背理法ではないが背理法とよく似たものとを、人はしばしば混同していることがあるそうで、周知の論法ではあるものの、背理法が何であるかについては注意が必要です。See Sara Negri and Jan von Plato, Proof Analysis: A Contribution to Hilbert's Last Problem, Cambridge University Press, 2011, p. 22, Jan von Plato, Elements of Logical Reasoning, Cambridge University Press, 2013, p. 81. 2016年2月3日追記: 次も参照ください。高崎金久、『学んでみよう! 記号論理』、日本評論社、2014年、79-81ページ、特に80ページ。追記終わり。
*3:ヤン・ルカシェーヴィッチ、「命題論理の多値の体系についての哲学的諸考察」、坂井秀寿訳、『論理思想の革命 理性の分析』、石本新編、東海大学出版会、1972年、161ページ。
*4:もう一つは、Euclid です。彼の『原論』、第IX巻、命題12です。William Kneale and Martha Kneale, The Development of Logic, Oxford University Press, 1962, p. 174, n. 3, また、本文中、後掲の Kneale 論文、p. 63, および次を参照。Ignacio Angelelli, ''Two Attempts to Disenchant the ''Consequentia Mirabilis'','' in: Günter Löffladt hg., Mathematik - Logik - Philosophie: Ideen und ihre historischen Wechselwirkungen, Harri Deutsch, Europa-Nr.: 56061, 2012, pp. 64-65, <http://www.utexas.edu/cola/_files/iaa4774/Two_attempts_to_disenchant_the_consequentia_mirabilis.pdf>. ただし、『原論』、IX, 12 で本当に consequentia mirabilis が使われているのかどうかについては疑問があります。Euclid は consequentia mirabilis を明示的に定式化しているわけではないし、この論法の名前にはっきりと言及しながら問題の命題12を証明しているわけでもありません。See Angelelli, p. 64. 数学史家の幾人かは、件の命題12の証明の解説において、consequentia mirabilis にまったく言及していません。例えば、斎藤憲先生は、問題の命題12の解説において、まったく consequentia mirabilis に触れていません。エウクレイデス、『原論 VII-X』、斎藤憲訳、解説、エウクレイデス全集 第2巻、東京大学出版会、2015年、37-38, 245-246ページ。斎藤先生によると、命題12の証明で使われている論法は、帰謬法/背理法であり、かつ現在の私たちからすればですが、primitive な「数学的帰納法の一種」だということです。『原論 VII-X』、245-246ページ。しかしそこでの「証明は非常に混乱している」のだそうです。『原論 VII-X』、37ページ。次の本で IX, 12 の解説を見ても、Ian Mueller, Philosophy of Mathematics and Deductive Structure in Euclid's Elements, Dover Publications, 2006, first published in 1981, p. 100, consequentia mirabilis への言及はありません。Mueller 先生も IX, 12 の証明は confused だと述べておられます。Ibid. 私自身は、IX, 12 の証明を読んでも、確かに consequentia mirabilis が使われているという感じがあまりしません。背理法のように見えます。しかし背理法による証明が終わった後にもまだなぜか証明が続いており、冗長で混乱した印象を受けます。Angelelli 先生は、背理法のように見えるがそうではなく、consequentia mirabilis が使われているのであって、冗長な部分は、別の人間による加筆、改竄であると述べておられます。Angelelli, p. 65. 本文中、後掲の Kneale 論文でもこの問題に言及されており、Kneale 先生も、IX, 12 で使われているのは背理法ではなく、consequentia mirabilis だとされ、冗長に見える部分にはある役割が存在するとしています。Kneale, p. 63. その役割については、別途取り上げる必要のある内容なので、この後、本文の「3.2. 背理法と consequentia mirabilis の関係」において触れることにします。なお、consequentia mirabilis の淵源の一つは Euclid の『原論』であると述べましたが、そもそも IX, 12 は後世における追加ではないかとの疑念も持ち上がっています。『原論 VII-X』、38ページ、脚注35, 249, 277ページ参照。IX, 12 が後世における追加であるならば、たとえ IX, 12 で consequentia mirabilis が使われているとしても、IX, 12 がその淵源の一つとはならないかもしれません。
*5:Kneale, p. 62. 簡単に日本語に訳すと、次のような感じになるでしょうか。少し開き気味に訳します。「哲学せねばならないとするのなら、哲学せねばならない。哲学すべきでないとするのなら、哲学せねばならない (すべきでないという理由を考えるのに哲学せねばならないから)。それ故いずれにせよ、哲学せねばならない。」 誤訳があれば、ご容赦ください。余談ですが、「哲学なんて役に立たないからいらない、そんなのやらなくていい」と述べる方には、この Aristotle の論法で切り返すことができるかもしれません。すなわち、「貴殿のご意見では、哲学なんてしなくてよいとのことである。しかし、そもそも哲学をやるべきであるならばやるべきである、だが、やらなくていいのなら、やらなくていいという理由を語らねばならず、それを語ることは哲学的営みに他ならないから、やるべきである、いずれにせよ結局哲学はやるべきであって、必要なのである」と。でも、このように切り返すときっと逆上されるとは思うし、まぁ、完璧な切り返しとも言えませんが…。閑話休題。ちなみにここでの Aristotle の論証は、彼の Protrepticus に載っているとのことです。Kneale, p. 62. Protrepticus についてはその英訳暫定版が、PDF で net を通じて誰でも無料で閲覧できるようになっています。次がそれです。Aristotle, Protrepticus: A Reconstruction of Aristotle's Lost Dialogue, by D. S. Hutchinson and Monte Ransome Johnson, 2015, <http://www.protrepticus.info/protreprecon2015i20.pdf>. ただし、いくつかの単語を使ってこの文書に検索をかけてみても、問題の Aristotle の言葉 'If we ought to philosophise, ... ' はヒットしないようです。また、日本語訳としては、アリストテレス、『哲学のすすめ』、廣川洋一訳、解説、講談社学術文庫、講談社、2011年がありますが、これに軽く目を通してみた限りでは「哲学すべきであるならば、哲学すべきであり、哲学すべきでないならば、云々」という文は出てこないように見受けられます。なぜ英訳にも和訳にも問題の文章が出てこないのかに関しては、正確なところはわかりませんが、そもそも Protrepticus は後代の人間が、編者それぞれの基準に基づいて Aristotle の文とされるものを集めてきてまとめたものですから、誰がどのような基準で編集するかによって、本の内容が異なってくることが上げられるかもしれません。このこと故に、英訳でも和訳でも問題の文が現れないのかもしれません。追記2018年12月2日: 問題の日本語訳は、刊行されたばかりの次の著作に、いくつか見られます。アリストテレス、『著作断片集 2』、新版 アリストテレス全集 第20巻、岩波書店、2018年、60-63ページ。追記終り。
*6:Kneale, p. 62.
*7:Ibid., the argument (iv).
*8:Ibid., the argument (v).
*9:Kneale, p. 63, the formula (viii).
*10:Kneale, p. 63.
*11:論証 not-not-P, ∴P を許す規則に対し、「2重否定除去の規則」、「2重否定除去則」などと呼び、式 'not-not-P ならば P' を「2重否定の除去の法則」などと呼び、前者が論証で後者が式であるため、互いに区別されますが、一方から他方への書き換えは容易にできますので、問題は生じませんから、以下ではしばしば無差別に語ります。
*12:前原、56-57ページ。1967年版から。2005年版も同ページ。
*13:前原、57ページ。1967年版から。2005年版も同ページ。
*14:前原、56, 181ページ。2005年版も同ページ。前原先生の証明図に対し、引用者による補足を一部加えて引用します。
*15:前原、57-58ページ。1967年版から引用。2005年版も同ページ。前原先生の証明図に補足を入れて引用します。
*16:背理法原理、排中律、2重否定除去則 (と「両刀論法の規則」と呼ばれるもの) が、どれも互いに証明できるということは、次でも示されています。N. W. テニント、『自然演繹の論理学』、藤村龍雄訳、八千代出版、1981年、72-73, 61-62ページ、東条敏、『言語・知識・信念の論理』、知の科学シリーズ、オーム社、2006年、62-65ページ。また、両刀論法の規則/排中律の規則 (the rule of excluded middle) と背理法との関係については、次も参照。Sara Negri and Jan von Plato, Structural Proof Theory, Cambridge University Press, 2001, pp. 203-205, 12, and Ditto, Proof Analysis, 2011, pp. 21-23. この他に、2重否定除去の法則、背理法、排中律の関係については、以下も参照。J. von Plato, Elements of Logical Reasoning, 2013, pp. 80-83. 2016年1月3日追記: 背理法原理、排中律、2重否定除去則がお互いに証明できることは、おそらくよく読まれている論理学の教科書である次の本でも示されています。戸田山和久、『論理学をつくる』、名古屋大学出版会、2000年、232-233, 296-297, 418ページ。追記終わり。
*17:Dag Prawitz, Natural Deduction: A Proof-Theoretical Study, Almqvist and Wiksell, Acta Universitatis Stockholmiensis/Stockholm Studies in Philosophy, vol. 3, 1965, p. 20, Also Dover Publications Edition, 2006, p. 20.
*18:歴史的にはこの第二型を、(単独の式としての) consequentia mirabilis とすることはおそらくできないでしょうが、今はそのことは問いません。次を参照。ルカシェーヴィッチ、「命題論理の多値の体系についての哲学的諸考察」、Angelelli, ''Two Attempts to Disenchant the ''Consequentia Mirabilis''.''
*19:背理法原理第二型は、実際には背理法に対応しないし、背理法を式にしたものとは言えません。よって背理法原理の名にふさわしくないのですが、ここではそのことは問わないことにします。See Negri and von Plato, Proof Analysis, 2011, p. 22, von Plato, Elements of Logical Reasoning, 2013, p. 81. 2016年2月3日追記: 次も参照ください。高崎金久、『学んでみよう! 記号論理』、79-81ページ、特に80ページ。追記終わり。